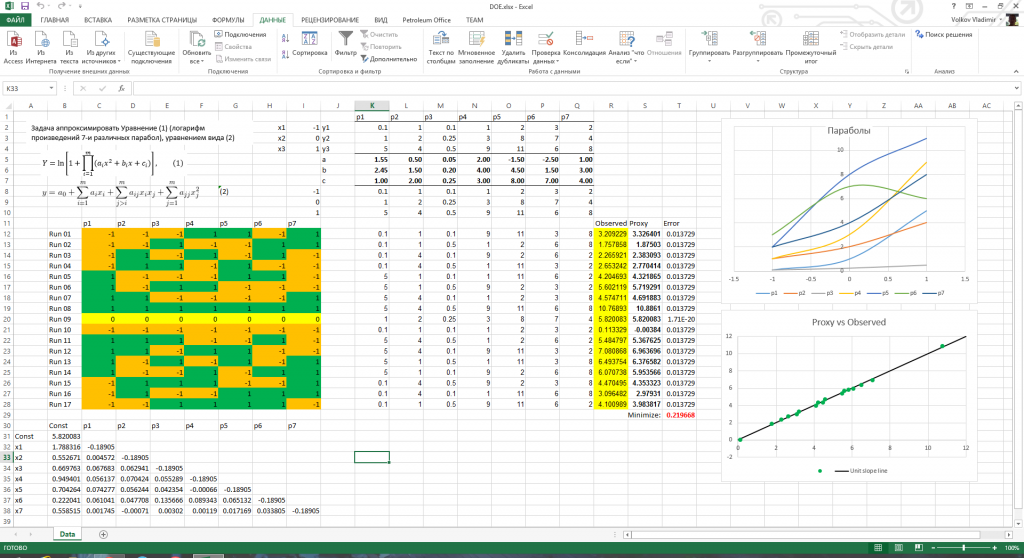
Тема планирования эксперимента (Design of Experiment) вызвала некоторый интерес. После вопроса о том, как выполняется нелинейная регрессия и используется ли для этого специализированный софт, я решил написать что-то вроде мини инструкции, как это может быть реализовано в Excel без необходимости приобритения коммерческих add-in или наличия специализированного софта. В принципе все, что было описано ранее в первом топике о планировании эксперимента, можно реализовать, используя лишь стандартные возможности Excel, не прибегая ни к каким стронним продуктам. Единственный add-in, которым нужно будет воспользоваться это Solver (или в русской версии офиса – Поиск Решений). Он входит в стандартный набор и уже предустановлен. Для его использования нужно лишь в Параметрах Excel в разделе Надстройки, после нажатия на кнопку Перейти… (Go…) в нижней части окна, в появившемся диалоговом окне выбрать его в списке адд-инов (вот блин тяжела работа тех, кто составляет мануалы к программам). Это верно для 2013 офиса, в более ранних последовательность действий чуть отличается, но суть одна. После того, как вы это сделаете, на панели Данные в правой ее части появится дополнительная секция – Анализ с кнопкой “Поиск решения” (на скриншоте ниже видна эта кнопка):
Для демонстрации того как это может быть реализовано в Excel, я решил попробовать аппроксимировать простенькую функцию, представлющую собой логарифм произведений парабол, заданных на отрезке [-1,1]:
![]()
Для некоторого подобия нефтяным задачам, параболы в интервале [-1;1] были выбраны возрастающими (кроме одной, для проверки точности аппроксимирующей функции). Таким образом значения параболы при x=-1 представляет собой пессимистичную оценку, при +1 оптимистичную, 0 – базовый (средний) вариант
Таблицу с планом Плакетта-Бермана, для 7 параметров гуглим в интернете, находим где должны быть +1, а где -1 и воспроизводим в Excel. Стандарный план Plackett-Burman представляет собой лишь верхнюю часть таблицы (до строчки с нулями), мы его немного расширили, сделав так называемый зеркальный план. Симметрично скопировав верхнюю часть (для малоопытных в Экселе, делаем Копировать-Вставить, затем копируем -1 из любой ячейки, делаем Скопировать-Специальная вставка – Значения / Умножить), получаем зеркальный план, который лучше подходит для нелинейных задач.
В таблице ниже вводим значения коэффициентов прокси-функции. В данном случае это будет нижне-диагональная матрица, элементы которой являются коэффициентами следующего уравнения:
![Rendered by QuickLaTeX.com \[y=a_0+\sum_{i=1}^{m}a_{i}x_{i}+\sum_{j>i}^{m}a_{ij}x_{i}x_{j}+\sum_{j=1}^{m}a_{jj}x_{j}^{2}\]](http://volvlad.com/wp-content/ql-cache/quicklatex.com-1d546c39e5d93d377b6ccd1323e62463_l3.png)
Для начала присваиваем 0 всем значения этой матрицы. Затем записываем формулу, рассчитывающую значения прокси-функции по значениям параметров (+1 и -1) с использованием коэффициентов матрицы (столбец S примера).
Для того, чтобы начать регрессию коэффициентов, нам нужно будет также задать целевую функцию, которую нужно минимизировать. В этом случае это будет сумма квадратов ошибок ![]()
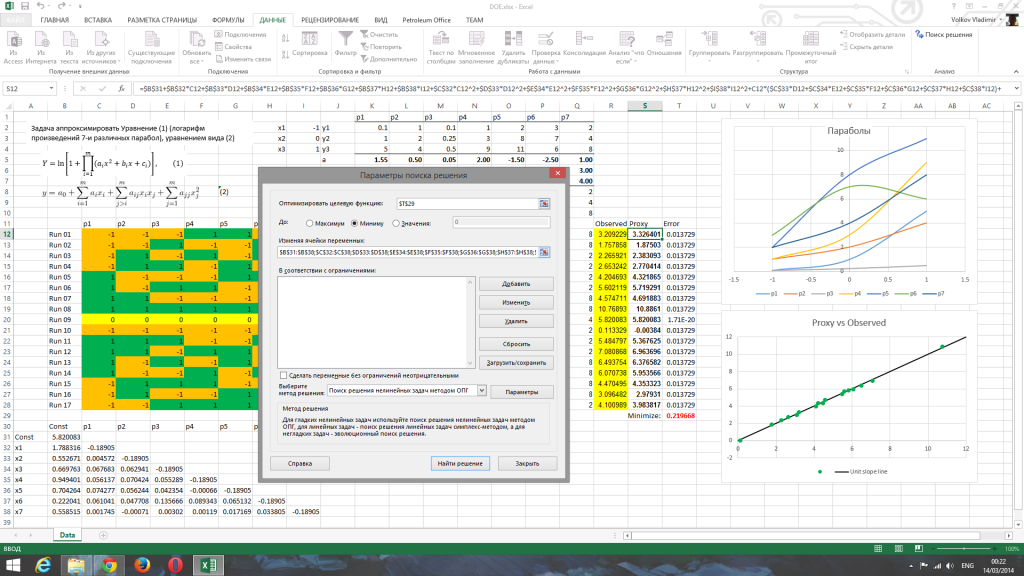
После того, как все функции заданы, осталось лишь запустить линейную регрессию. На панели Данные, запускаем поиск решения. В появившемся окне, в поле “Минимизировать целевую функцию” выбираем ячейку с суммой квадратов ошибок (ячейка Т29 в примере). Выбираем цель – Минимум. В поле “Изменяя ячейки переменных” выбираем столбцы нижне-диагональной матрицы. В качестве метода решения выбираем “метод ОПГ”. И нажимаем кнопку “Найти решение”. Спустя несколько секунд коэффициенты будут найдены. Как видно из графика справа, значения прокси-функции и точные значения исходной функции имеют очень хорошую корреляцию.
Следующий шаг, запуск моделирования Монте-Карло я описывать не буду.
Файл с описанным примером, вышлю по запросу каждому желающему.


Приветсвую, Влад!
Вышли, пож-та, пример на ramazanovdn@gmail.com
Спасибо!
Отправил. Прошу прощения за поздний ответ, спамеры атаковали, не заметил этот комментарий за тонной спама. Переставил спам-фильтр. Теперь должно наладится.
Влад, добрый день,
Вышли пож-та файл с описанием. Тема очень прикладная и интересная!
Спасибо
Отправил
Ничего не пришло ( Не могли бы выслать еще раз)
Здравствуйте!
Вышлите, пожалуйста, файл для ознакомления.
Спасибо!
Добрый день!
Вышли пожалуйста файл с примером на seropian_roman@yahoo.com
Заранее спасибо!
Выслал всем
Доброго времени суток. Скиньте плз.
Добрый день!
Можно мне тоже файл с примером на kynzevichVitaliy@gmail.com
Заранее спасибо!
Отправил
Владимир, добрый день
Можно выслать Excel на a-gubaev@mail.ru.
Буду очень благодарен!
Здравствуйте.
Влад, очень интересно пишете, пожалуйста продолжайте.
Прошу выслать файл с примером leontyev.ivan@gmail.com
Спасибо!
Здравствуйте! Случайно нашла эту тему. Если автор ее еще читает, вышлите, пожалуйста, мне тоже работу на amina.talipova@gmail.com
Выслал всем.
Здравствуйте.
Можно выслать Excel на kennho8@gmail.com
Заранее спасибо!
Здравствуйте.
Можно выслать Excel jamshed8808@mail.ru
Заранее спасибо!
Добрый день!
А можно выслать файл на почту.
Отправил на почту.