Пожалуй, начнем так – “Вы все еще монтекарлите традиционным способом, тогда мы идем к вам”.
В этом посте я хочу рассказать о применении метода планирования эксперимента (design of experiments) для проведения анализа неопределенностей. В большинстве случаев, когда результат, зависимый от нескольких неопределенных параметров, нельзя получить спустя несколько секунд после изменения входных данных, я предпочитаю пользоваться этим методом. Это позволяет значительно экономить время и при этом получать весьма хорошие результаты.
Сначала предыстория. Месяц назад нужно было в срочном порядке вставить новую ранее не утвержденную скважину в программу бурения. На данный момент согласно нашей модели скважина выглядит весьма привлекательно, более того по запасам и стартовому дебиту лучше всех остальных скважин. При этом скважина будет расположена в той части, в которой до сих пор имеются достаточно высокие неопределенности по пористости, NTG, проницаемости, трещиноватости, наличию или отсутствию высокопроводимых каналов, вертикальной анизотропии (Kv/Kh) и пр. В общем, у многих есть сомнения на счет того, что это лучшая скважина в проекте.
Модель на которой базируются все наши расчеты, точнее говоря три версии модели – пессимистическая, наиболее вероятная и оптимистическая (Low, Mid and High) – заматчены на историю с учетом результатов сейсмики 4D. И в целом по всему месторождению эти варианты модели примерно соотносятся по запасам с P90, P50 и Р10. Детальное вероятностное моделирование было проведено несколько лет назад, и после этого не было очень серьезных правок.
Но получилось так, что в зоне расположения этой скважины разбег по свойствам оказался минимальным, что в принципе ничему не противоречит. В результате, накопленная добыча этой скважины не очень сильно отличалась по все трем вариантам (тут надо заметить, что речь идет об инкрементальной добыче – думаю, что об этом надо отдельный пост написать как-нибудь). Минимальный разбег по вариантам, никого не устраивал, поэтому было решено провести детальный анализ неопределенности, но только в той части пласта, в которой будет расположена скважина, чтобы не разрушать адаптацию модели. К счастью, эта часть пласта практически не взаимодействовала с разрабатываемой частью месторождения, поэтому любые махинации со свойствами не очень сильно влияли на работу существующих скважин.
При традиционном моделировании Монте-Карло, для того чтобы получить хоть какое-то представление о функции распределения запасов скважины (в данном случае речь идет о накопленных запасах скважины), пришлось было бы провести не одну сотню расчетов. А учитывая, что в нашем случае результат нужно было получить, проведя расчеты в симуляторе, затрачивая по 2 часа на вариант с максимумом 5 параллельных расчетов на кластере, то заняло бы это достаточно долгое время. Тратить рабочее время на подобные расчеты представляется крайне непрактичным.
В данном случае планирование эксперимента является отличным способом, позволяющим значительно сократить количество расчетов (в нашем случае – кол-во запусков модели), а также, что тоже немаловажно количество необходимых входных данных.
Не вдаваясь особо в детали и выражаясь простым языком, скажу, что суть метода заключается в следующем (тут мы перейдем на понятный для нефтяников язык, с примерами) – для каждого из неопределенных параметров (таких как, например – пористость, NTG, водонасыщенность, проницаемость, уровень ВНК, концевые точки фазовых проницаемостей, и пр.) задаются возможные границы от минимума до максимума. Различные комбинации, которых дают определенное значение выходной функции – STOIIP, извлекаемые запасы, и т.д. Также стоит отметить, что границы минимумов и максимумов по возможности нужно задать шире, чтобы покрыть весь диапазон возможных значений. Чтобы был покрыт интервал со значениями вероятностей от близких к 0 до близких к 100%. Т.е. другими словами нужно сгененировать дополнительно к среднему, еще два детерминистических варианта Low-Low и High-High.
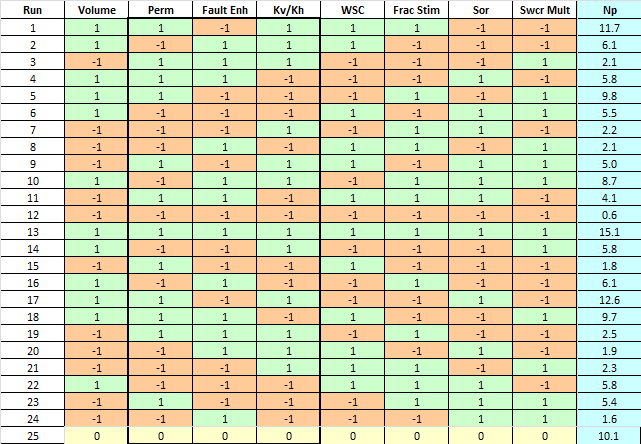
В таблице плана эксперимента минимальное значение параметра представлено, как (-1), а максимальное (+1), 0 – соответственно представляет собой середину.
Если пропустить тот факт, что при планировании эксперимента в зависимости от решаемых задач применяются различные способы построения таблицы планов для наших нефтяных задач очень хорошо подходит метод Plackett-Burman (PB). Почитать о нем можно, к примеру тут: http://www.itl.nist.gov/div898/handbook/pri/section3/pri335.htm. В этом плане для оценки N факторов используется всего N+1 запусков.
Первая строка матрицы плана задается в виде (пример для m=11): ![]() . Затем каждая следующая строчка матрицы образуется из предыдущей циклическим сдвигом вправо. Последняя строка (m+1) состоит из (-1). Как правило, к этому плану добавляются еще две строчки с +1 и центральная точка – 0, которая также используется для проверки адекватности прокси.
. Затем каждая следующая строчка матрицы образуется из предыдущей циклическим сдвигом вправо. Последняя строка (m+1) состоит из (-1). Как правило, к этому плану добавляются еще две строчки с +1 и центральная точка – 0, которая также используется для проверки адекватности прокси.
Но также следует отметить, что в чистом виде Plackett-Burman, как правило используется лишь для первоначальной оценки при проведении эксперимента, чтобы выявить наиболее важные параметры и отсеять параметры незначительным образом влияющие на конечный результат.
Однако, если в качестве плана использовать, так называемый зеркальный план (Folded Plackett-Burman), с добавлением центрального элемента (строчки с нулями), то результат с достаточно высокой достоверностью может быть представлен аппроксимирующей функцией в виде полигона второй степени с взаимодействующими компонентами (проще формулой написать чем словами выразить). Ну и разумеется нужно будет выполнить в 2 раза больше расчетов:
![Rendered by QuickLaTeX.com \[y=a_0+\sum_{i=1}^{m}a_{i}x_{i}+\sum_{j>i}^{m}a_{ij}x_{i}x_{j}+\sum_{j=1}^{m}a_{jj}x_{j}^{2}\]](http://volvlad.com/wp-content/ql-cache/quicklatex.com-1d546c39e5d93d377b6ccd1323e62463_l3.png)
Этим уравнением хорошо аппроксимируются функции следующего вида:
В примере с нашей скважиной, я выбрал следующие неопределенные параметры:
- Поровый объем (по сути объединение пористости, NTG, толщины)
- Проницаемость
- kv/Kh
- Проницаемость вдоль разломов
- Критическая водонасыщенность (наличие эффекта пропитки)
- Остаточная нефтенасыщенность
- Наличие каналов прорыва воды от нагнетательных скважин (water short-circuits)
- Успешность стимуляции скважины (насколько хорошо будет проведен кислотный ГРП).
Выходной параметр один – накопленная добыча скважины.
Для этого случая Folded Plackett-Burman план выглядит таким образом:
Затем генерируем и запускаем на расчет 25 моделей, представляющие собой каждую из строк плана. Результаты расчетов заносим в таблицу. После запуска макроса выполняющего регрессию находим уравнение аппроксимирующее результаты полученные на модели. Сравниваем результаты полученные по модели и по прокси-функции и оцениваем качество аппроксимации.
Также после получения прокси-функции неплохо выполнить проверку репрезентативности модели, для этого нужно запусть несколько вариантов с центральными (0) и дробными значениями факторов и сравнить результаты предсказанные прокси-функцией и полученные на модели. Если расхождение допустимо, то смело можно использовать нашу функцию для дальнейшего вероятностного анализа методом Монте-Карло.
Зеленые точки это 25 вариантов, которые использовались для нахождения прокси-функции, а красные точки – это варианты модели, запущенные для проверки прокси-функции (наиболее влиятельные фаторы были взяты равным 0). Видно, что прокси несколько недооценивает запасы скважины для этих случаев.
Поэтому следующим шагом был запуск нахождения новой прокси-функции с использованием этих дополнительных точек. На следующей картинке видно, что результат улучшился. Дополнительная красная точка, это проверка модели для эксперимента с дробными значениями факторов.
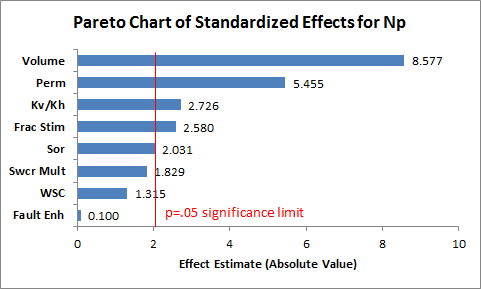
Если посмотреть на диаграмму Парето, то видно, что в этом случае наиболее влиятельными оказались – объемы (геологические запасы), проницаемость, Kv/Kh, эффективность проведения стимуляции и примерно одинаковое влияние оказывают значения остаточной нефтенасыщенности и критической водонасыщенности (что в принципе было ожидаемо, т.к. они одинаковым образом масштабируют кривые фазовых проницаемостей). Наличие высокопроводимых каналов не оказывает существенного влияния на добычу нефти, хотя сильно влияет на обводненность. Ну и самый интересный параметр – высокая проводимость вдоль разломов, которая в некоторых местах подтверждена сейсмикой 4D, по данному графику не оказывает практически никакого влияния. Но на самом деле, получилось так, что слишком сильное увеличение проницаемости вдоль разломов, а также польное отсутствие увеличения проницаемости (проницаемость такая же как и в районах удаленных от разломов) оказывают негативное влияние на запасы. Т.е. хорошо иметь некоторое увеличение проводимости.
Для найденной прокси-функции запускаем традиционное моделирование Монте-Карло. Для этого задаем распределения вероятностей наших факторов, зная каким значениям соответсвуют +1, 0 и -1 для каждого из факторов несложно подобрать границы. Также стоит сказать, что значения могут выходить за границы [-1,+1], но усугублять этим не стоит, т.к. во-первых при выборе минимальных/максимальных значений мы руководствовались правилом, чтобы эти значени соответствовали вероятностям близким к 0. А во-вторых экстраполяция хуже работает по сравнению с интерполяцией.
Вот что получилось в итоге:
Ну и напоследок, необходимо вабрать варианты, которые будут представлять Р10, Р50 и Р90. Подставляя различные значения факторов в прокси-функцию, находим такие комбинации параметров, которые примерно дают значения соответствующие Р10, Р50 и Р90.
Еще несколько рекомендаций по выбору функций распределения. Как правило для оценки запасов чаще всего используются 4 распределения – треугольное, лог-нормальное, нормальное, равномерное. Треугольное чаще используется для пористости, NTG, Sw, RF, при этом очень часто используется скошенное (несимметричное) распределение. Нормальные распределения использются для отражения меньшей изменчиваости параметра относительно среднего и они всегда симметричны. Лог-нормальное часто используется в поиске при оценке общих объемов залежи (площадь, толщины), где нередки широкие диапазоны потенциальных значений (часто различающихся на порядки). Также если к примеру проанализировать размер всех месторождений в некотором отдельно выбранном бассейне, то они как правило имеют лог-нормальное распределение, что подтверждает праильность допущения об использовании лог-нормального распределения. Или другими словами, это означает, что найденное месторождение вероятнее окажется более мелким чем огромным. После открытия месторождения, как правило, лог-нормальное распределение заменяется треугольным. Хотя если разобраться, то большой разницы нет. Лог-нормальное и относительно узким диапазоном значений дает в итоге примерно такое же распределение, как и треугольное. Если мы вообще ничего не знаем о распределении, а также не имеем никакого представления о среднем значении параметра, но знаем лишь максимум и минимум, то нужно использовать равномерное распределение.





Отличная статья! Давно хотел разобраться с этим, никак не находлось подходящих источников..
Скажите, а Вы сами всему доучиваетесь или это западная система тренингов такая – необходимо разобраться с технологией эксперимента – вот вам курс, учитесь?
Ссылки на источники где-то есть, могу поискать и скинуть. С дизайном эксперимента, когда-то давно разбирался сам. Плюс у нас в компании этот метод очень часто применяется, что-то вроде стандарта.
А в остальном, что-то на курсах, что-то сам изучаю, по разному. Курсы два-три раза в год, больше обычно не бывает.
Скиньте пожалуста ссылки на источники, буду благодарен
Молодец, Вован! 🙂
Сделать работу обычно мотивации хватает, а вот описать и поделиться с народом обычно уже лень. Большой респект тебе.
Из своего опыта добавлю по части равномерного распределения – не стоит этим злоупотреблять! И с максимально широкими границами диапазонов тоже не соглашусь. Если приходится использовать такие вещи – значит информации слишком мало.
И анализ неопределенности покажет, что “завтра температура воздуха будет от минус 100 до плюс 100” 🙂
Я именно это и имел в виду, что если по какому-то параметру вообще ничего не известно, или вероятность того, что все будет хорошо или слишком плохо примерно одинакова, то берем равномерное распределение.
По поводу широких диапазонов урезать всегда можно. Да и очень часто проблема анализа неопределенностей, приводит к слишком узкому диапазону значений.
Мне вот это непонятно:
Для найденной прокси-функции запускаем традиционное моделирование Монте-Карло. Для этого задаем распределения вероятностей наших факторов, зная каким значениям соответсвуют +1, 0 и -1 для каждого из факторов несложно подобрать границы.
Как полученная прокси учитывается при последующем Монте-Карло? а если не учитывается, то зачем она нужна, если все равно Монте-Карло считать, можно же было сразу монтекарлить.
И кстати, в каком софте считали неопределенность? в Петреле же есть прокси моделирование, интересно как там устроено, автоматически регрессия считается? (у самого у меня петреля нету проверить как работает)
Монте-Карло выполняется для найденной прокси-функции, где каждый неопределенный параметр изменяется от -1 до +1 (ну можно еще немного выйти за пределы, скажем, до 1.5 но без фанатизма, экстраполяция как правило хуже интерполяции). К примеру, допустим, что мы хотим оценить неопределенность STOIIP. Для простоты, рассмотрим на примере одного из неопределенных параметров – пористости. К примеру, мы знаем, что она у нас находится где-то в пределах от 15% до 25% со средним 20%, тогда в прокси-функции -1 соответствует 15%, 0 – 20%, а 25% это +1. Для Монте-Карло, распределение будет задавать для параметра отвечающего пористости в пределах от -1 до +1. По остальным параметрам делаем то же самое.
Со STOIIP конечно же все просто, перемножим все неопределенные параметры мы получим результат через доли секунды и в реальной жизни использовать планирование эксперимента и нахождение прокси-функции нецелесообразно. Но если для решения задачи требуется значительно время, т.е. если скажем ответ можно получить лишь запустив симулятор, то тогда планирование эксперимента неплохой способ оценки неопределенности
Монте-Карло моделирование я делал в Crystal Ball, но можно и в любом другом софте.
Регрессию мы тоже выполняем с помощью Эксел адд-ина, но можно и без него.
(Ответил с опозданием, т.е. пропустил комментарий, среди тонны спама, где-то дыра в спам-фильтре, надо будет обновить).
По части p-уровней значимости –
раньше, как нас учили, это было почти обязательно.
Но сейчас – проверка значимости не особо нужна, ни на что в общем-то не влияет.
Прохожу курс от Стэнфорда – https://class.stanford.edu/courses/HumanitiesScience/StatLearning/Winter2014/,
там на форуме нашел кое-каие статьи (на линкед-ин тоже об этом пишут):
http://www.nature.com/news/scientific-method-statistical-errors-1.14700
http://robjhyndman.com/papers/sst2.pdf
ЗЫ> Мы учили мат.статистику 15 лет назад. Но не все было фундаментально!