В нефтяной индустрии мы крайне редко работаем с точными данными, напротив практически всегда нам приходится иметь дело с неопределенностью и рисками. Не заостряя внимание на различии между анализом неопределенности и рисками, но для того чтобы понять о чем пойдет речь, определим для себя, что под анализом рисков будем понимать применение анализа для определения, описания и оценки неопределенности и ее влияния на проекты. Для решения подобных задач в нашем распоряжении есть множество инструментов. Выбор инструмента анализа во многом зависит от решаемой задачи. И как правило, если предстоит осуществлять выбор между некими альтернативами, то применяются деревья решений. А если же нужно просто оценить масштабы неопределенности, то выбирается моделирование методом Монте-Карло. Однако, применение метода Монте-Карло требует большого числа реализаций, что не всегда возможно с практической точки зрения, в случае если например для получения результата нужно запускать на расчет гидродинамическую модель.
В этих случаях часто применяется дискретизация непрерывного распределения с помощью дерева решений. Существует много различных способов дискретизации, наиболее часто используемыми являются трехточечные методы со значениями “25-50-25” или “30-40-30” (Среднее Свонсона).
При этом происходит следующее: Кривая непрерывного распределения (синяя) заменяется дискретной (оранжевой).
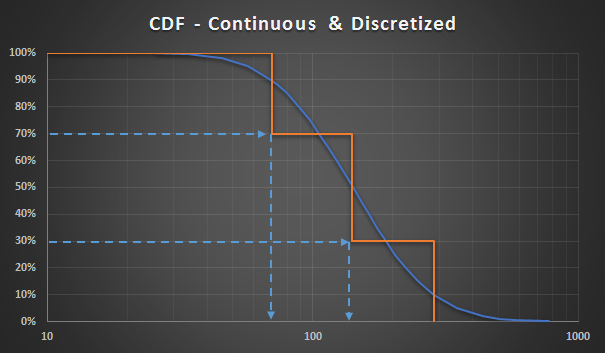
На картинке выше кажется, что метод слишком упрощает представление случайной величины и не может в полной мере представить все разнообразие возможных значений. Однако, это не совсем так. Главная задача дискретизации сохранить форму распределения и его ключевые моменты (mean, std.dev) и перцентили (страшно звучит по-русски) (P90, P10). Ну и самое важное, чтобы это упрощение не повлияло на результат в принятии решения.
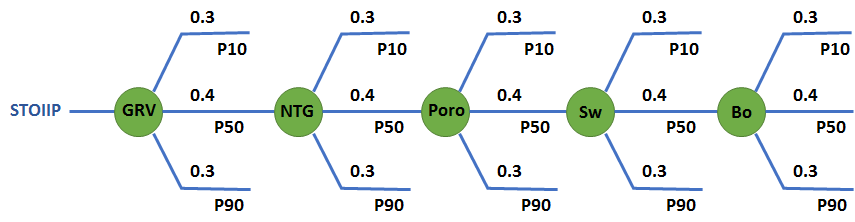
Рассмотрим простой пример, в котором рассчитываются геологические запасы – STOIIP. Все входные переменные будут случайными величинами – объем месторождения, NTG, средняя пористость, насыщенность, и объемный коэффициент нефти. Для простоты все входные параметры кроме GRV зададим в виде нормальных распределений. Так как STOIIP является произведением этих параметров, то итоговое распределение будет стремиться к лог-нормальному распределению.
Произведем 2 расчета. Первый, 10000 реализаций по методу Монте-Карло, где каждый входной параметр задан своей непрерывной функцией распределения. И второй, методом дерева решений, где входные параметры дискретизированы по правилу 30-40-30:
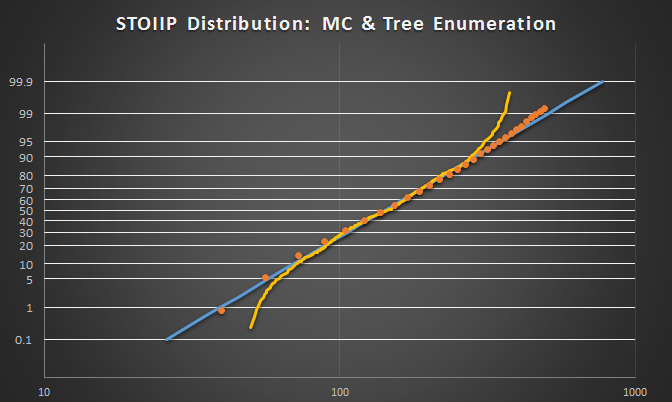
В результате, графики распределения вероятности STOIIP будут выглядеть следующим образом:
Прямая линия – теоретическая кривая лог-нормального распределения построенная по заданным mean и std.dev. Точки – распределение STOIIP, полученное методом Монте-Карло (10000 реализаций). Кривая золотистого цвета – распределение построенное по дереву решений обходом всех возможных вариантов.
Видно, что при дискретизации очень хорошо предсказываются Mean и скажем P50. Значения P90 и P10 получены с меньшей точностью. И значительные расхождения наблюдаются для краевых перцетилей (<P10, >P90). Т.е. диапазон значений при данном методе дискретизации уменьшается. Но учитывая, что мы чаще всего смотрим на P10, P50 и P90 – результат очень даже неплохой.
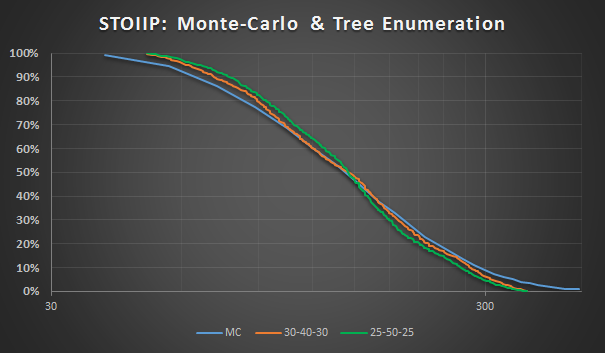
И еще, ниже приведено сравнение дискретизации 25-50-25 и 30-40-30. Видно, что для лог-нормального распределения часто применяемое многими правило 25-50-25 в гораздо большей степени занижает отклонение значений STOIIP от мат.ожидания, чем 30-40-30: